Whether you're a forex trader, a bond trader, or a stock trader, your goal ultimately is to make money with the least amount of risk. For those in the options markets, the most important and easiest principle they can understand to achieve this is the put-call parity.
In today's article, we'll focus on the nuts and bolts of this potentially lucrative put-call parity concept and also take a look at some examples. But before we do that, we must get the basics right to ensure we're all on the same page. Let's start with what options are, the way they work, and everything that's involved.
Also Read: What Is Covered Put Strategy: Comprehensive Guide
Contents
- What Are Options?
- What Is a Put-Call Parity?
- Calculating Put-Call Parity
- Example of a Put-Call Parity
- Why Put-Call Parity Matters
- FAQs
- Conclusion
What Are Options?
Options are contracts that give their holders the right, but not the obligation, to sell or buy an underlying asset, like a stock, at a specific price by an expiration day or within a certain period of time.
If the holder doesn't exercise the option before it hits its expiration date, the option becomes valueless, and they can no longer do so. Typically, each options contract controls 100 shares of a specific underlying asset.
Also worth noting, there are two kinds of options: Call and put options.
- Put Option
Put options are contracts tied to stocks. You pay a premium for one of such contracts, and it gives you the right to sell the stock at a predetermined price, known as the strike price. You're given the freedom to execute the contract at any point you wish as long as it hasn't hit its expiration day.
If the stock price decreases enough, then you have the opportunity to sell your put option for a profit. You won't be obligated to execute the put contract. So, in case the stock price doesn't drop enough, you can always let the contract expire, which means you'll only lose the premium you paid.
A breakeven point in put options is the difference between the premium and the strike price.
I'll give you an example. Imagine Amazon trades at $120 per share, but you think it's overvalued. In that case, you decide to buy a put option contract with a strike price of $100 and a 3-months expiration. The premium costs $2 per share. Here, the breakeven point would be $98, the difference between the $100 strike price and the $2 premium. If the stock price plummets to $50, then you're up $48 per share.
- Call Option
A call option is also a contract tied to an underlying stock. You pay a premium for these contracts, which gives you the right, but not the obligation, to buy the underlying security at a predetermined strike price any time you wish before the contract expires.
If the stock's price increases enough, you either sell the contract or execute it at a profit. If it does not, then you let it expire and only lose the premium that you paid.
The breakeven point on call options is the premium and strike price sum. You can always calculate your call option's profit or loss at any point by subtracting the stock's current price from the breakeven point.
Now that you understand what options are and what call and put options mean, we can skip to the most exciting section of the post and discuss put-call parity.
What Is a Put-Call Parity?
In efficient markets, a portfolio holding both a short put and a long call option for an identical asset, expiration date, and the same strike price should generate a similar amount as the portfolio holding an equal futures contract long position.
That's what is called a “put-call parity,” and the following equation expresses it.
Short Put Return + Long Call Return = the Long Future Return.
Basically, whatever profit you gain from selling a put option and buying a matching call option needs to be the same as what you'll earn if you take an equivalent trade through a futures contract.
The relationship still holds even when the positions are inverted as follows:
Long Put Return + Short Call Return = the Short Future Return.
We'll check out an example in a minute. First, we'll need to look at the complete put-call parity formula. This will help you, a trader, use put-call options to set your pricing.
Calculating Put-Call Parity
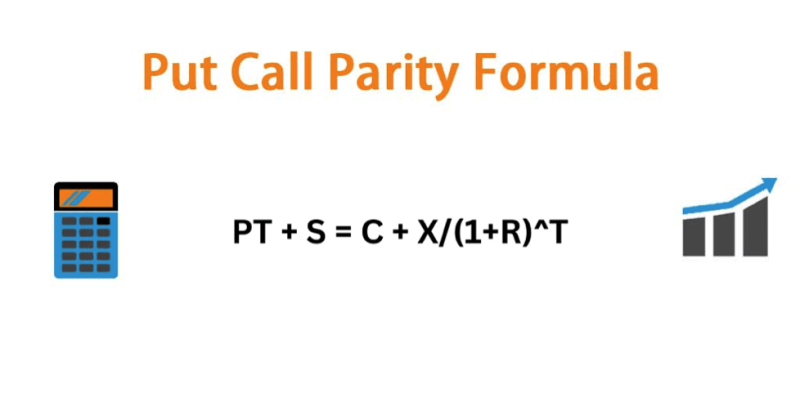
To better understand Put-Call parity, we'll need to take a look at its full formula:
PT + S = C + X/(1+R)^T
Here is what each of these letters stands for.
- T stands for the time of expiration, which is expressed as an exponent
- R is the risk-free rate
- X is the exercise or strike price
- C is the premium for the call option
- S is the current market price for the asset
- PT is the premium for the put option.
To understand the significance of this put-call parity equation and the world of Put-Call Parity in general, you'll need a detailed put-call parity example.
Example of a Put-Call Parity
So, let's assume shares for XYZ have a present value of $25 each. Assuming that no transacting costs are charged, then you have two potential portfolios you can set up.
First, you could set up a futures contract to buy XYZ shares for $30 in six months. Second, you could set up a short put option on XYZ shares for $30 with an expiration in six months and set up a long call option on the stock for $30 with the expiration date also in half a year.
In both contracts in the second scenario, the price, or premium, is $5.
So, let's say that XYZ's share price rises to $$40. In that case, in the 1st portfolio, your long call position permits you to buy XYZ's stock for $30 against a $40 underlying asset, which means you net a $10 profit.
If you picked the second portfolio, then the put option you sold expired unclaimed and “out of the money,” leaving you the premium you make from the contract, which is $5. You'll then exercise your long call option and buy the stock for $30. This means you make $10 in profit minus the $5 premium you already paid, leaving you with a net gain of $5.
At the end of the day, you're left with a $10 premium that you made across the entire position.
Now, let's assume the share price for XYZ fell to $20.
In that case, in the 1st portfolio, your long call position will require you to purchase XYZ's shares for $30 against a $20 underlying asset, leaving you with a net loss of $10.
In the 1st portfolio, however, the trader handling the put option exercises their option and sells you XYZ's stock at $30, meaning you'll lose $10, but minus the premium you collect worth $5. This leaves you with a -$5. Your long position will expire out of the money, and you'll lose the $5 premium the contract costs you. At the end of the day, this leaves you with a $10 loss across the position.
This option trading relationship remains consistent in an efficient market. Now, onto why Put-Call Parity matters.
Why Put-Call Parity Matters
The formula we looked at earlier allows you to assess returns on a put option and a call option when compared to investing in a different, safe option. As for the free risk rate, most investors generally use returns on 3-month U.S. T-bills (Treasury bills.)
What's more? In the example above, we've used the same option premiums for the call as well as the put contracts. This results in parity in a hypothetical market with no risk or additional market activity. That said, the actual market isn't so nicely balanced.
In the real market, options premiums are priced depending on the safe, alternative investments one could instead make, as well as the likelihood that they'll expire in the money.
All this implies that as an options trader, the complete put-call parity equation allows you to gauge the approximate value of a call or put relative to its other components and decide how you can balance the premiums appropriately.
Let's briefly return to the earlier example earlier. XYZ stocks' present value is $25 each, and our options boast a $30 strike price and a six-month (0.5) year expiration date. I'll assume a 3 percent risk-free rate. In that case, we'd calculate the premiums as shown.
PT + 25 = C + 30/(1+0.03)^0.5
PT + 25 = C + 30/(1.03)^0.5
PT + 25 = C + 30/1.0148
PT + 25 = C + 29.56
PT – C = 29.56 – 25
PT – C = 4.56
In the real market, you should price your put options $4.56 higher than your call option price. This will reflect the risk that, compared to the call, the put option will close in the money. The absence of parity between the top options means a perfect arbitrage opportunity exists.
Arbitrage is a strategy that exploits price variances in assets in different markets. For instance, let's say that the share of company XYZ is trading at $30 on NASDAQ. At the same time, the XYZ stock is listed on the London Stock Exchange at $25.
As a trader, you can purchase the stock through the London Stock Exchange for $25 and sell it through the NASDAQ for $30. That arbitrage opportunity ought to earn you a profit of $5 per share.
I know all these processes and strategies sound highly complicated, but they can be equally lucrative once you master them.
FAQs
How Are Options Priced?
The price of an option is the sum of its intrinsic value, which is the difference between the underlying asset's current price and the option's strike price as well as time value. Time value is directly related to the remaining time before the option expires.
What is a Conversion?
A conversion is an investment strategy in which a short call and long put on the same underlying security and with the same expiration date and the same strike are combined with a long stock position. This strategy is also known as conversion arbitrage.
Conclusion
Options trading isn't for every individual trader or investor. It requires way more knowledge and attention than ordinary bond and stock investing, which is why it tends to prove challenging for most individuals.
That said, for institutional investors, accredited investors, or even individual investors who decide to delve deeper into the realm and are looking for investment advice, put-call parity is a crucial concept they'll need to master. It describes the practical equivalence between put and call options with the same expiration date, time value, and of similar assets.
You can rest assured that understanding the put-call parity principle will open the door to booking profits whenever put and call options aren't in parity. HAPPY TRADING!!
















